Chapter 1. Umbrella sampling
Article still brewing… 🍵
In the meantime, you might want to check the tutorial (from 33:02) on umbrella sampling that I contributed to the iCoMSE workshop on advanced sampling!
Eager for the article to be published? Just fill out this quick form and I’ll deliver the tutorial straight to your inbox as soon as it goes live! Your keen interest might just be the nudge I need to get it finished sooner! if you have any question, feel free to drop me a line at wei-tse.hsu@bioch.ox.ac.uk!
0. Learning objectives
Upon completion of this chapter, the student should be able to:
- Comprehend the theory behind umbrella sampling
- Perform umbrella sampling to estimate the free energy surface along chosen degrees of freedom
- Modify the parameters of umbrella sampling if the results are not ideal

1. Theory
Umbrella sampling1,2, one of the earliest enhanced sampling methods, has proven useful for estimating the free energy as a function of chosen collective variables (CVs). By imposing restraint potentials centered at different values of chosen CVs, umbrella sampling forces the system to sample different regions in the CV space, ultimately allowing the estimation of the free energy profile. The protocol of performing umbrella sampling consists of two steps: the pulling simulation and the production simulation. Using the example of computing free energy as a function of the ion-pair distance of NaCl, we will discuss these two steps in detail in the following subsections.
1-1. Pulling simulation
A pulling simulation, also known as a steered MD simulation, involves exerting a pulling force between specific groups of atom(s) (termed the pull groups) during the simulation. As the applied force pulls apart the pull groups, the system is allowed to sample configurations with vaying CV values. The purpose of the pulling simulation is to extract a series of configurations of the system characterized by different values of CVs, which then serve to seed the production simulation in the next step. Mathematically, given a force constant
As an example, here we consider the dissociation process of NaCl, where the most intuitive CV is the ion-pair distance. During a pulling simulation, to enable NaCl to visit configurations having different ion-pair distances, one can define the pull groups as the sodium and the chloride ions, then exert a pulling force between them. To make the pulling easier, one can choose to fix the position of the sodium ion using a position restraint, while pulling the chloride ion away. This process is illustrated in Figure 1, within which a number of configurations are extracted from the trajectory of the pulling simulation. These configurations (47 configurations in our case having ion-pair distances
Supplementary note: Position restraints implemented in GROMACS
A position restraint is a potential that restrain a particle to a fixed reference position, usually the initial position. In GROMACS, the most common form of a position restraint is a harmonic potential, which can be expressed as follows:
Conceptually, a position restraint is an energy penalty incurred when the particle deviates from the reference position. Given a fixed force constant, a larger deviation will lead to a higher energy penalty. This energy penalty is added to the system’s potential energy, hence making it less likely for the particle to be found away from the reference position.
In addition to the harmonic position restraint, GROMACS also supports a flat-bottom position restraint, which penalizes the particle only when it deviates beyond a certain distance from the reference position. Notably, there are also different types of restraints available in GROMACS, such as angle restraints, dihedral restraints, distance restraints, and orientation restraints. For more details, please refer to the GROMACS reference manual. In Section 2.2.1 in this tutorial, we will show how one can set up a position restraint in GROMACS.
- Distance restraint in the production simulation
- Other CV -> Other restraints, not necessarily a distance restraint
1-2. Production simulations
In this step, a standard MD simulations is performed for each configuration generated from the pulling simulation (e.g., 47 simulations in total for the 47 windows in Figure 1). A bias potential (or biasing potential), usually a restraint potential centered at the CV values of the starting configuration, is applied during each simulation. The bias potential can take various forms depending on the CVs of interest. In umbrella sampling, a common choice is to use a harmonic restraint for each window. Mathematically, we have the bias potential
Importantly, since the force constants
Supplementary note: Why is it important to have sufficient overlap between neighboring windows?
Adaquate overlap between neighboring windows avoids gaps in the phase space coverage and ensures ample sampling for the transition regions between windows. The overlap regions are necessary for free energy estimators such as WHAM, TI, BAR, and MBAR. They allow these methods to estimate expectations from one distribution from another, stitching together the individual window distributions into a single unbiased distribution, which can then be converted to the free energy profile. If the overlap is insufficient, one may end up having higher uncertainty in the free energy profile for the tail-end regions of each distribution due to a lower number of uncorrelated samples.
👨💻 Exercise 1
In the second window shown in Figure 1, what is the incurred energy penality if the ion-pair distance
Click here for the solution.
As shown in Figure 1, the center of the second window,
2. Tutorial 🧑🏻🏫
In this exercise, our goal is to perform umbrella sampling for NaCl to compute its free energy as a function of the ion-pair distance, which is an intuitive CV relevant to the dissociation process of NaCl. This exercise is accompanied by the jupyter notebook umbrella_sampling.ipynb in the folder Chapter_1 in the course repository. If you have all the software prerequisites installed, you can run each Bash and Python commands in the command line and the Python console, respectively. Otherwise, you can simply launch the tutorial on Binder () without installing anything. Note that in the Binder notebook, MPI-enabled GROMACS patched with PLUMED 2.8.0 is used, though we will not use any functionalities from PLUMED in this tutorial. Throughout the tutorial, we assume that the working directory is
Chapter_1 unless otherwise noted. All GROMACS commands in the notebook assume MPI-enabled GROMACS is available and they are launched by mpirun with the number of MPI processes (-np) specified. You can choose to use tMPI-based GROMACS on your local machine if you prefer, though the simulation time may vary.
2.1. Setting up
In the folder Systems/NaCl in the course repository, you can find simulation inputs we need for this tutorial, though some will need some modifications later in this tutorial. These input files include NaCl.gro, NaCl.top, and MD_NVT.mdp. If you are interested in more details about how these files are obtained or generated, please refer to the README file for the system.
To get started, we remove the output folders/files of the exercise with the following Bash commands, in case there are any from previous runs:
dirs=(sim_* pull *mdp *dat)
for dir in "${dirs[@]}"; do
if ls -d "$dir" >/dev/null 2>&1; then
rm -rf "$dir"
fi
done
In Sections 2.2 and 2.3, we will perform the pulling simulation and the production simulation, respectively.
2.2. Pulling simulation
As a reminder, the purpose of a pulling simulation is to generate configurations with different values of CV (the ion-pair distance in our case). The generated configurations will then be used as the initial configurations in the subsequent production simulations. In a pulling simulation, we need to make the following two decisions:
- Defining the pull groups: The pull groups are groups of atoms between which we exert the pulling force. Here, we define the sodium and chloride ions as the pull groups. In GROMACS, this setup can be done by adding pull codes to the
.mdpfile, as we will elaborate in Section 2.2.2. - Choosing the immobile group: In a pulling simulation, it is common to apply a position restraint to one of the pull groups to make the pulling process more efficient. In our case, we will choose to fix the position of the sodium ion while pulling the chloride ion away (as shown in Figure 1), but reversing the mobile and immobile groups should not make a difference in the resulting free energy profile. As we will see in Section 2.2.1, the application of the position restraint can be done by modifying the
.topfile.
Here, we first create a folder pull specifically for the pulling simulation, and copy over NaCl.gro from the folder Systems/NaCl:
mkdir pull
cp ../Systems/NaCl/NaCl.gro pull/.
In the following subsections, we will modify the .top file and the .mdp file to apply a position restraint and set up the pull code, respectively.
2.2.1. Modification of the .top file
The .top file we have in Systems/NaCl, NaCl.top, is for standard MD simulations, which has the following content:
#include "oplsaa.ff/forcefield.itp"
#include "oplsaa.ff/tip3p.itp"
[ moleculetype ]
; molname nrexcl
CL 1
[ atoms ]
; id at type res nr residu name at name cg nr charge mass
1 opls_401 1 CL CL 1 -1 35.45300
[ moleculetype ]
; molname nrexcl
NA 1
[ atoms ]
; id at type res nr residu name at name cg nr charge mass
1 opls_407 1 NA NA 1 1 22.98977
[ System ]
NaCl in water
[ Molecules ]
SOL 107
NA 1
CL 1
To apply a position restraint, one needs to add the following lines before the [ System ] directive. (In the notebook, we save the .top file as NaCl_US.top in the folder pull.)
; position restraints for Na
# ifdef POSRES_NA
# include "Na_posres.itp"
# endif
These lines mean that if the variable POSRES_NA is defined in the .mdp file for the pulling simulation, the position restraint defined in the file Na_posres.itp will be activated. Here, we can generate the .itp file Na_posres.itp and saved it in the folder pull using the following Bash commands. (For more details about GROMACS .itp file and the ifdef statments, please refer to the GROMACS reference manual.)
echo '[ position_restraints ]
; i funct fcx fcy fcz
1 1 1000 1000 1000' > pull/Na_posres.itp
Here are more details about the columns in the [ position_restraints ] directive:
i: The index of the atom (in the[ moleculetype ]directive) to which the position restraint is applied. Note that the[ position_restraints ]directive is under the[ moleculetype ]directive, so even if the index of the sodium ion inNaCl.grois 322, it is the first (and only) atom in the[ moleculetype ]that corresponds toNA, so we specify the value ofias 1 (instead of 322) here.funct: The function type of the restraint. Type1corresponds to a harmonic potential in the form of Equation[ moleculetype ]directive, please visit the GROMACS reference manual.fcx,fcy, andfcz: The force constants
Notably, in more complicated cases, such as pulling two chains of protein molecules apart, you may need to restrain not just one atom (as in our example here) but multiple ones, in which case the GROMACS genrestr command could be useful. For more details, please check the Supplementary note below.
Supplementary note: Generating an .itp file using the GROMACS genrestr command
In addition to manually writing an .itp file like we did above, one can alternatively generate an .itp file for position restraints by using the GROMACS genrestr command, which requires an input .ndx file (the so-called index file) if the atoms to be restrained are not defined in any default index groups. In our case, we can create an .ndx file and add an index group for the sodium ion by executing the following command:
mpirun -np 1 gmx_mpi make_ndx -f pull/NaCl.gro -o pull/NaCl.ndx
Then, in the interactive prompt, enter a 322 (to select atom 322, which is the sodium ion), then name 6 NA (to rename Group 6 (created by a 322) as NA), and finally q (to save and quit). With the index file, we can then run the following command (and select Group 6 (NA)) to generate an .itp file:
mpirun -np 1 gmx_mpi genrestr -f pull/NaCl.gro -n pull/NaCl.ndx -o pull/Na_posres.itp
Note that in this case, the value of i in the [ position_restraints ] directive in the output .itp file would be 322, so we still need to manually change it to 1.
2.2.2. Modification of the .mdp file
Here, we will create the .mdp file for the pulling simulation (saved in the folder pull as NaCl_pull.mdp) by modifying the .mdp template for standard molecular dynamics, MD-NVT.mdp in Systems/NaCl. The .mdp template has the following parameters:
integrator = md
dt = 0.002
nsteps = 250000
cutoff-scheme = Verlet
coulombtype = PME
rlist = 0.6
rcoulomb = 0.6
rvdw = 0.6
constraints = h-bonds
tcoupl = V-rescale
ref_t = 300
tau-t = 1.0
tc-grps = System
gen-vel = yes
gen-temp = 300
gen-seed = -1
DispCorr = AllEnerPres
nstxout-compressed = 50
nstxout = 50000
nstvout = 50000
Note that here we adopt smaller cutoffs than usual for the neighbor list (rlist) and for the interactions (rcoulomb and rvdw) just so that we can use a smaller simulation box for the system, which makes the example simulation affordable even on a laptop. We set the simulation length as 250 ps, which should be sufficient for our case. In addition, the simulation will be performed in the NVT ensemble.
To suit the need of running a pulling simulation, we first need to define POSRES_NA in the .mdp file so the position restraint is activated. This can be done by adding the following line to the .mdp file.
define=-DPOSRES_NA
Then, to pull the chloride ion away, we need to add the following pull code to the .mdp file:
; Pull code
pull = yes ; Activate the pull code
pull-ncoords = 1 ; Here we only have 1 CV
pull-ngroups = 2 ; We have 2 pull groups
pull-group1-name = NA ; index 1
pull-group2-name = CL ; index 2
pull-coord1-groups = 1 2 ; groups with indices 1 (NA) and 2 (CL) are involved
pull-coord1-type = umbrella ; The umbrella potential (i.e., harmonic potential) is used.
pull-coord1-geometry = distance ; Pull along the vector connecting the two groups
pull-coord1-dim = Y Y Y ; Dimensions that the pull coordinate acts on
pull-coord1-start = yes ; The harmonic potential is centered at the initial COM distance
pull-coord1-rate = 0.0010 ; 0.0010 nm/ps -> A deviation of 0.25 nm in a 250 ps-simulation
pull-coord1-k = 1000 ; units: kJ/mol/nm^2
As shown above, parameters in the code block come with simple explanations. Below are some additional explanations for some of the parameters:
pull-coord1-init: This parameter is not explicitly specified in the.mdpfile above and will hence by taken as 0 by default, in which case we essentially define the initial pull distance as a distance of 0.pull-coord1-start: If this parameter is set toyes, GROMACS will add the pull distance (the distance between the COM of the pull groups) of the starting conformation topull-coord1-init. This means that in cases wherepull-coord1-initis set to 0,pull-coord1-start = yeswill set the center of the harmonic potential to the initial COM distance, i.e. any configuration is restrained to the initial configuration.pull-coord1-start = nowill restrain any configuration to zero pull distance, a case where the pull groups are on top of each other.
How we should specify the parameters
pull-coord1-initandpull-coord1-startdepends on what configuration we want to restrain any other configuration to. In the pulling simulation here, whetherpull-coord1-startis set toyesornodoes not matter However, as we will discuss later, the parameterpull-coord1-startmust be set toyesin the production run.pull-coord1-rate: The rate at which the imaginary spring attached between the ions is elongated.- Importantly, the pull distance must not exceed half of the smallest dimension of the simulation box, which is 0.7248 nnm in our case. (As can be checked in
pull/NaCl.gro, the simulation box we use is a cubic box with a side length of 1.48561 nm.) This is to prevent the pull group from interacting with the periodic image of the system. - Here, we set
pull-coord1-rate = 0.0010in a 250 ps-simulation, so the expected elongation should be around 0.25 nm. In the extreme case where the force constant of the position restraint is infinity such that the sodium ion is completed fixed, the maximal pull distance should be approximately 0.53 nm. As we are using a relatively force constant of 1000
Considering the reference/initial pull distance of 0.28 nm (as can be calculated from the 3D coordinates of Na and Cl ions in
pull/NaCl.gro), we should leave enough bufferAs can be calculated from the 3D coordinates of Na and Cl ions in
pull/NaCl.gro, the reference/initial pull distance is around 0.28 nm.- Importantly, the pull distance must not exceed half of the smallest dimension of the simulation box, which is 0.7248 nnm in our case. (As can be checked in
Here, we set pull-coord1-rate = 0.0010 in a 250 ps-simulation
Since we set pull-coord1-rate = 0.0010 in a 250 ps-simulation, the expected elongation should be around 0.25 nm. In an extreme case
Therefore, an elongation of 0.25 nm (which can be achieved by setting pull-coord1-rate = 0.0010 in a 250 ps-simulation, as done in our case) should be safe,
, as it will lead to a maximal pull distance of 0.53 nm approximately.
pull-coord1-k: The force constant does not really matter in the pulling simulation, since we set a non-zeropull-coord1-rate, which should allow configurations with different pull distances anyway.
For other possible options/parameters for pulling, please refer to the GROMACS reference manual.
2.2.3. Running the pulling simulation
With all the input files prepared in the pull folder (including NaCl.gro, NaCl.top, and NaCl_pull.mdp), we can finally run the pulling simulation. Note that depending on the version of GROMACS you are using, you might need a different grompp command.
Versions earlier than 2022
Simply execute the following command should be fine:
mpirun -np 1 gmx_mpi grompp -f pull/NaCl_pull.mdp -c pull/NaCl.gro -r pull/NaCl.gro -p pull/NaCl_US.top -o pull/pull.tpr -po pull/mdout.mdp -maxwarn 1 mpirun -np 1 gmx_mpi mdrun -deffnm pull/pull -pf pull/pullf.xvg -px pull/pullx.xvg -ntomp 1Note that in the Binder notebook, GROMACS 2021.4 is used, so the above commands should work.
Versions later than 2022
If your are using GROMACS with a version later than 2022, the
gromppcommand above might fail with the following error:Fatal error: Group NA referenced in the .mdp file was not found in the index file. Group names must match either [moleculetype] names or custom index group names, in which case you must supply an index file to the '-n' option of grompp.To resolve this, we need to create an index file where both the groups
NAandCLreferenced bypull-group1-nameandpull-group2-namein the.mdpfile are availble, then pass the index file to thegromppcommand. To do this, execute the following command:mpirun -np 1 gmx_mpi make_ndx -f pull/NaCl.gro -o pull/NaCl.ndxThen, in the interactive prompt, enter the following:
a 322: To select atom 322, which is the sodium ionname 6 NA: To rename Group 6 (created bya 322) asNAa 323: To select atom 323, which is the chloride ionname 7 CL: To rename Group 7 (created bya 323) asCLq: To save and quit
Or, you can just execute the following command without interacting with the prompt:
echo -e 'a 322\nname 6 NA\na323\nname 7 CL\nq' | mpirun -np 1 gmx_mpi make_ndx -f pull/NaCl.gro -o pull/NaCl.ndxAfter creating
NaCl.ndx, we then pass it to thegromppcommand with the-nflag, so the commands for running the pulling simulation would be as follows. (Themdruncommand is the same for both scenarios.)mpirun -np 1 gmx_mpi grompp -f pull/NaCl_pull.mdp -c pull/NaCl.gro -r pull/NaCl.gro -p pull/NaCl_US.top -o pull/pull.tpr -po pull/mdout.mdp -maxwarn 1 mpirun -np 1 gmx_mpi mdrun -deffnm pull/pull -pf pull/pullf.xvg -px pull/pullx.xvg -ntomp 1
Notably, in both cases, pull/NaCl.gro is passed to the grompp command via the -r flag, from which the reference/initial pull distance is calculated for the restraint. On Binder, the mdrun command above should take around 40 seconds to complete. If you are running the simulation on your local machine, the time might vary depending on the hardware you are using.
Compared to a standard MD simulation, a pulling simulation has two additional output files: pullf.xvg and pullx.xvg, which document the time series of the pulling force and the pull distance, i.e. ion-pair distance. In the next subsection, we will need pullx.xvg to decide what configurations to extract from the pulling simulation.
2.2.4. Generation of the initial configurations for the production run
Before generating configurations from the pulling simulation, we first need to decide the number of windows to use for the production run. This requires experience and sometimes trials and errors, but the general goal is to ensure that the CV distributions of neighboring windows have sufficient overlap. For simple systems like NaCl, 8 windows should be sufficient. For more complicated cases where you might want to sample a wider range of CV values or even have multiple CVs, you might need more windows.
To determine the center of each window, it is common to simply divide the CV range linearly, which might not always be optimal but should serve as a decent starting point. In our case, we define the equally spaced centers with the ion-pair distance ranging from the minimum value observed in the pulling simulation up to 0.6 nm. Depending on the force constants we want to use in the next section for umbrella localization, the center of the last window, hence its probability distribution, should not be too close to the upper bound (i.e., 0.7248 nm) so that a configuration with a CV value exceeding the upper bound is unlikely.
Below we use a Python script to identify the time frames in the pulling simulation at which the configuration has a CV value close to the desired value, i.e., the predefined center of the window.
import numpy as np
pullx = np.transpose(np.loadtxt('pull/pullx.xvg', comments=['@', '#']))
t, dist = pullx[0], pullx[1]
centers = np.linspace(min(dist), 0.6, 8) # the spacing between windows should be around 0.05 nm
diff_list = np.abs([dist - i for i in centers])
diff_idx = [np.argmin(diff_list[i]) for i in range(len(centers))] # dist[diff_idx]: distances closet to the centers
t_extract = t[diff_idx] # in ps
print(f'The ion-pair distances (in nm) of the chosen configurations are: {dist[diff_idx]}')
print(f'The initial configurations will be extracted from the following time frames (in ps): {t_extract}')
The script should give STDOUT like below:
The ion-pair distances (in nm) of the chosen configurations are: [0.248848 0.29903 0.349314 0.39936 0.449456 0.499348 0.549502 0.599458]
The initial configurations will be extracted from the following time frames (in ps): [ 28.8 58.8 128.1 100.2 139.3 156.6 235.6 247.3]
Note that you may get slightly different values for the chosen ion-pair distances due to the randomness of the simulation, but the centers should roughly be at 0.25 nm, 0.30 nm, …, 0.60 nm, respectively. Then, to extract the configurations corresponding to the chosen time frames, we run the following Python script:
import os
for i in range(len(t_extract)):
os.mkdir(f'sim_{i}')
os.system(f'echo System | mpirun -np 1 gmx_mpi trjconv -s pull/pull.tpr -f pull/pull.xtc -dump {t_extract[i]} -o sim_{i}/NaCl_{i}.gro')
Upon completion of the script, you should have folders named in the form of sim_*, with a .gro file NaCl_*.gro in each of them. These 8 folders correspond to the 8 windows that we will use in the production simulaitons, which are seeded by the .gro files in the folders.
2.3. Production run
In the previous step, we have prepared the 8 input .gro files for the 8 simulations in the production stage, which will use the same topology file NaCl_US.top as we used for the pulling simulation. Still, we need to prepare the .mdp file NaCl_umbrella.mdp shared by all the 8 simulations. Compared to the .mdp file we used for the pulling simulation, NaCl_umbrella.mdp has the following 3 differences:
- The simulation length is 500 ps instead of 250 ps.
- The pull rate is set as 0, since we need to localize each configuration at a different ion-pair distance.
- The force constant is set as 8000 instead of 1000
Notably, the force constants play an important role in localizing configurations at different CV values during the production stage. Specifically, the force constants should be large enough to prevent the configurations from drifting to the nearest metastable states, but also not too large so that the each CV distribution will not be too narrow to have sufficient overlap with its neighboring distributions. While for simple systems (like NaCl), it is possible to estimate reasonable force constants given the desired spread of the probability distributions, in most cases, the determination of the force constants still require some experience or trials and errors. In Exercise 3, we will explore how the force constant should be adjusted givne unsatisfactory distribution overlaps. Further in Section 2.5, we will discuss more in depth on how we can roughly estimate force constants to use in simple systems.
Another noteworthy thing is that pull-coord1-start is kept as yes here. Since each umbrella simulation has a different starting configuration, i.e., a different initial pull distance, using pull-coord1-start = yes means that configurations in the 1st, 2nd, …, and 8th window are restrained to
Now, to make necessary changes to the .mdp file, we can use the following commands:
cp pull/NaCl_pull.mdp NaCl_umbrella.mdp
sed -i -e "s/nsteps = 125000/nsteps = 250000/g" NaCl_umbrella.mdp # simulation length: 500 ps for each umbrella
sed -i -e "s/pull-coord1-rate = 0.0010 ; 0.0010 nm\/ps -> the pull distance in the 250 ps-simulation is 0.25 nm./pull-coord1-rate = 0/g" NaCl_umbrella.mdp
sed -i -e "s/pull-coord1-k = 1000 ; units: kJ\/mol\/nm^2/pull-coord1-k = 8000/g" NaCl_umbrella.mdp
All 8 simulations use the same .top file (which requires the .itp file Na_posres.itp) and .mdp file. In the script below, we distribute the input files to different sim_* folders, and for each of them, we run the GROMACS grompp command to generate the .tpr file and the mdrun command to run the simulation.
for i in {0..7}
do
cp pull/NaCl_US.top sim_${i}/. # Use the same top file as in the pulling simulation
cp pull/Na_posres.itp sim_${i}/. # Copy over the itp file for position restraint
cp pull/NaCl.ndx sim_${i}/. # This line is only needed for GROMACS with a version later than 2022
cp NaCl_umbrella.mdp sim_${i}/. # All simulations use the same .mdp file, NaCl_umbrella.mdp
cd sim_${i}
mpirun -np 1 gmx_mpi grompp -f NaCl_umbrella.mdp -c NaCl_${i}.gro -r NaCl_${i}.gro -p NaCl_US.top -o NaCl_US.tpr -n NaCl.ndx -maxwarn 1 # Generate the tpr
mpirun -np 1 gmx_mpi mdrun -deffnm NaCl_US -pf pullf.xvg -px pullx.xvg -ntomp 1
cd ../
done
The commands above assume a GROMACS version later than 2022. If you are using an earlier version, you don’t need to copy over the .ndx file and pass it to the grompp command. Notably, if you have more than 8 CPU cores, you can run all 8 simulations in parallel using the -multidir, which would be faster but also require MPI-enabled GROMACS.
mpirun -np 8 gmx_mpi mdrun -deffnm NaCl_US -pf pullf.xvg -px pullx.xvg -multidir sim_{0..7}
On my end, finishing all 8 simulations serially took less than 5 minutes, but depending on your hardware and whether you parallelize your simulations, the simulation time may vary.
👨💻 Exercise 2
Quick quesiton: What would happen if we set pull-coord1-init = 0 and pull-coord1-start = no in the production simulations?
Click here for the solution.
Setting pull-coord1-init = 0 and pull-coord1-start = no for all umbrella simulations will drive all configurations to have a pull distance of 0. Given that the associated metastable state has a non-zero pull distance (denoted as
would restrain all configurations to zero pull distance. Since for all configurations, the pull distance is always non-zero, all configurations are penalized depending their pull distances. Eventually, all distri
for all umbrella simulations, all configurations will be restra.
2.4. Data analysis
2.4.1. Distributions of the pulling distance
One indicator for assessing the quality of the production simulations and whether we need to adjust the parameters (e.g., the number of windows and force constants) is the overlap between neighboring replicas. Using the pullx.xvg file from each simulation in each folder, we can use the following code to visualize the distribution of the pulling distance for each simulation (Figure 2).
import matplotlib.pyplot as plt
pullx_data = [np.transpose(np.loadtxt(f'sim_{i}/pullx.xvg', comments=['@', '#'])) for i in range(8)]
dist_list = [data[1] for data in pullx_data]
plt.figure(figsize=(8, 3))
for i in range(8):
plt.hist(dist_list[i], bins=50, alpha=0.5)
plt.xlabel('Ion-pair distance (nm)')
plt.ylabel('Count')
plt.grid()
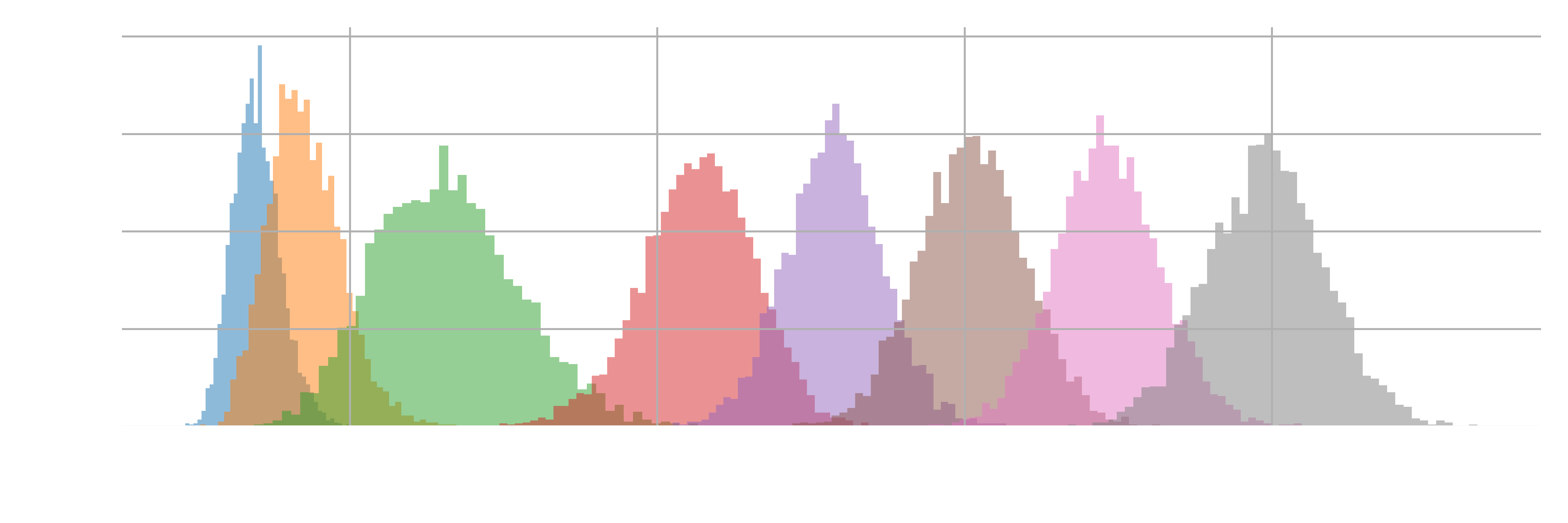
As shown in Figure 2, there is an overlap between every pair of neighboring windows, indicating that a force constant of 8000
👨💻 Exercise 3
An examination of Figure 2 shows that, although overlap exists between every pair of neighboring windows, the degree of overlap does vary. For instance, the overlap between the third and fourth windows is noticeably smaller than in other pairs, while the overlap between the initial two windows is significantly larger. Spend a minute or two to propose potential strategies to address this issue to achieve a more uniform overlap across all adjacent window pairs.
Click here for the solution.
Given that the centers of windows we specified were around 0.25 nm, 0.30 nm, …, 0.60 nm, it is clear from Figure 2 that a force constant of 8000
- Add one or more windows to the region where there is less overlap.
- For the windows whose distribution drifted away from its desired center, we can increase the force constant of the corresponding harmonic potential to better localize the configurations in the desired region. (Note that it is not required to use the same force constant across for all harmonic potentials!)
2.4.2. Free energy calculations
Once we have confirmed comprehensive coverage for the entire CV range of interest, we can proceed with free energy calculations. For umbrella sampling, various free energy estimators could be used, including WHAM, TI, BAR, MBAR, and others like UWHAM7, SWHAM8, and FastMBAR9. Since MBAR is provably the lowest variance unbiased estimator, we will use it here to perform free energy calculations. Though the theory underpinning MBAR may seem complicated, the Python package pymbar conveniently provides a straighforward implementation, simplifying our free energy calculation process. To install pymbar, execute:
pip install pymbar
Then, to perform free energy calculations and plot the free energy profile, run the following script.
import time
import pymbar
from pymbar import timeseries
import random
import scipy.stats
# Step 1: Setting up
K = 8 # number of umbrellas
N_max = 5001 # number of data points in each timeseries of ion-pair distance
kT = 1.381e-23 * 6.022e23 / 1000 * 300 # 1 kT converted to kJ/mol at 300 K
beta_k = np.ones(K) / kT # inverse temperature of simulations (in 1/(kJ/mol))
d_min, d_max = 0.25, 0.65 # minimum and maximum of the CV for plotting the FES
nbins = 50 # number of bins for FES
K_k = np.ones(K) * 8000 # spring constant (in kJ/mol/nm**2) for different simulations
N_k, g_k = np.zeros(K, int), np.zeros(K) # number of samples and statistical inefficiency of different simulations
d_kn = np.zeros([K, N_max]) # d_kn[k,n] is the ion-pair distance (in nm) for snapshot n from umbrella simulation k
u_kn = np.zeros([K, N_max]) # u_kn[k,n] is the reduced potential energy without umbrella restraints of snapshot n of umbrella simulation k
uncorrelated_samples = [] # Uncorrelated samples of different simulations
# Step 2: Read in and subsample the timeseries
for k in range(K):
d_kn[k] = np.transpose(np.loadtxt(f'sim_{k}/pullx.xvg', comments=['@', '#']))[1]
N_k[k] = len(d_kn[k])
d_temp = d_kn[k, 0:N_k[k]]
g_k[k] = timeseries.statistical_inefficiency(d_temp)
indices = timeseries.subsample_correlated_data(d_temp, g=g_k[k]) # indices of the uncorrelated samples
# Update u_kn and d_kn with uncorrelated samples
N_k[k] = len(indices) # At this point, N_k contains the number of uncorrelated samples for each state k
u_kn[k, 0:N_k[k]] = u_kn[k, indices]
d_kn[k, 0:N_k[k]] = d_kn[k, indices]
uncorrelated_samples.append(d_kn[k, indices])
d0_k = np.array([d_kn[i][0] for i in range(K)])
N_max = np.max(N_k) # shorten the array size
u_kln = np.zeros([K, K, N_max]) # u_kln[k,l,n] is the reduced potential energy of snapshot n from umbrella simulation k evaluated at umbrella l
u_kn -= u_kn.min() # shift the minimum of the FES to 0
# Step 3: Bin the data
bin_center_i = np.zeros([nbins])
bin_edges = np.linspace(d_min, d_max, nbins + 1)
for i in range(nbins):
bin_center_i[i] = 0.5 * (bin_edges[i] + bin_edges[i + 1])
# Step 4: Evaluate reduced energies in all umbrellas
for k in range(K):
for n in range(N_k[k]):
# Compute minimum-image ion-pair distance deviation from umbrella center l
dd = d_kn[k,n] - d0_k # delta d
# Compute energy of snapshot n from simulation k in umbrella potential l
u_kln[k,:,n] = u_kn[k,n] + beta_k[k] * (K_k / 2) * dd ** 2
# Step 5: Compute, output, and plot the FES
fes = pymbar.FES(u_kln, N_k, verbose=False)
histo_params = {'bin_edges': bin_edges}
d_n = pymbar.utils.kn_to_n(d_kn, N_k=N_k)
fes.generate_fes(u_kn, d_n, fes_type='histogram', histogram_parameters=histo_params)
results = fes.get_fes(bin_center_i, reference_point="from-lowest", uncertainty_method="analytical")
f_i = results["f_i"]
df_i = results["df_i"]
with open('fes.dat', 'w') as f:
f.write("# free energy profile (in units of kT), from histogramming\n")
f.write(f"# {'bin':>8s} {'f':>8s} {'df':>8s} \n")
for i in range(nbins):
f.write(f"{bin_center_i[i]:>8.3f} {f_i[i]:>8.3f} {df_i[i]:>8.3f} \n")
plt.figure()
plt.plot(bin_center_i, f_i)
plt.fill_between(bin_center_i, f_i - df_i, f_i + df_i, color='lightgreen')
plt.xlabel('Ion-pair distance (nm)')
plt.ylabel('Free energy (kT)')
plt.grid()
In summary, the script goes through the following steps:
- Step 1: Set up relevant parameters for the calculation, including the number of windows, the number of data points per window, simulation temperature, and so on.
- Step 2: Read in the time series of the ion-pair distance and decorrelate the data. Note that this step is important, since correlated samples would lead to underestimated uncertainty for the free energy profile.
- Step 3: Define bin centers for plotting the free energy profile. Note that MBAR does not use histograms and is therefore free from the histogram bias.
- Step 4: Evaluate the reduced energy for each umbrella window.
- Step 5: Compute the free energy profile, output
fes.datand plot the free energy profile.
Also, to plot the histograms of the number of uncorrelated samples for different CV values, one can use the following script:
plt.figure(figsize=(8, 3))
for i in range(8):
plt.hist(uncorrelated_samples[i], bins=50, alpha=0.5)
plt.xlabel('Ion-pair distance (nm)')
plt.ylabel('Number of uncorrelated samples')
plt.grid()
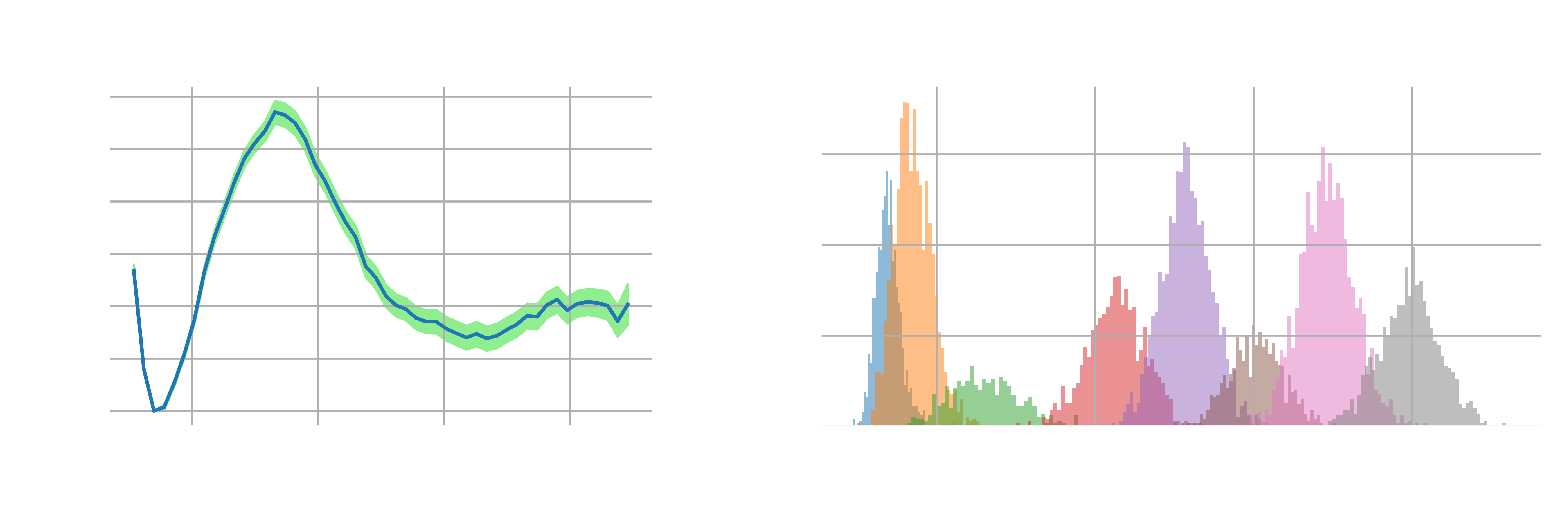
As a result, we plot the free energy as a function of the ion-pair distance of NaCl in panel A of Figure 3.
Notably, varying levels of uncertainty can arise at different CV values, which stems from different numbers of uncorrelated samples (due to different statistical inefficiencies/correlation times). For example, in the region characterized by an ion-pair distance around 0.25 nm, the uncertainty is minimal. In contrast, in regions corresponding to an ion-pair distance exceeding 0.6 nm, we observe a significant increase in uncertainty. This increased uncertainty is mainly attributable to the paucity of uncorrelated samples in these regions. In addition to adjust the number of windows/force constants, further extending the simulation should also reduce the uncertainty of the free energy profile.
2.5. Additional discussion
2.5.1. More about the force constant in umbrella sampling
In this section, we will explore more comprehensively about the role of force constants in umbrella sampling, or more generally, simulation methods in which we want to localize configurations in different regions of CV values, including replica exchange umbrella sampling introduced in Chapter 6. Before we dive into this section, let’s first look at the following exercise.
👨💻 Exercise 4
Rerun the production run twice, one with
Click here for the solution.
For the codes that run the umbrella sampling simulations with different force constants, please refer to the last section in the jupyter notebook. Note that you may need to tweak a few parameters in the code for free energy calculations to reflect the change in the force constant. For example, due to poor overlap, you may need to tweak the number of bins for calculating the free energy profile to avoid bins having no samples. As a result, we plot the free energy profiles and the histograms of uncorrelated samples for both cases, as shown in Figure E1.
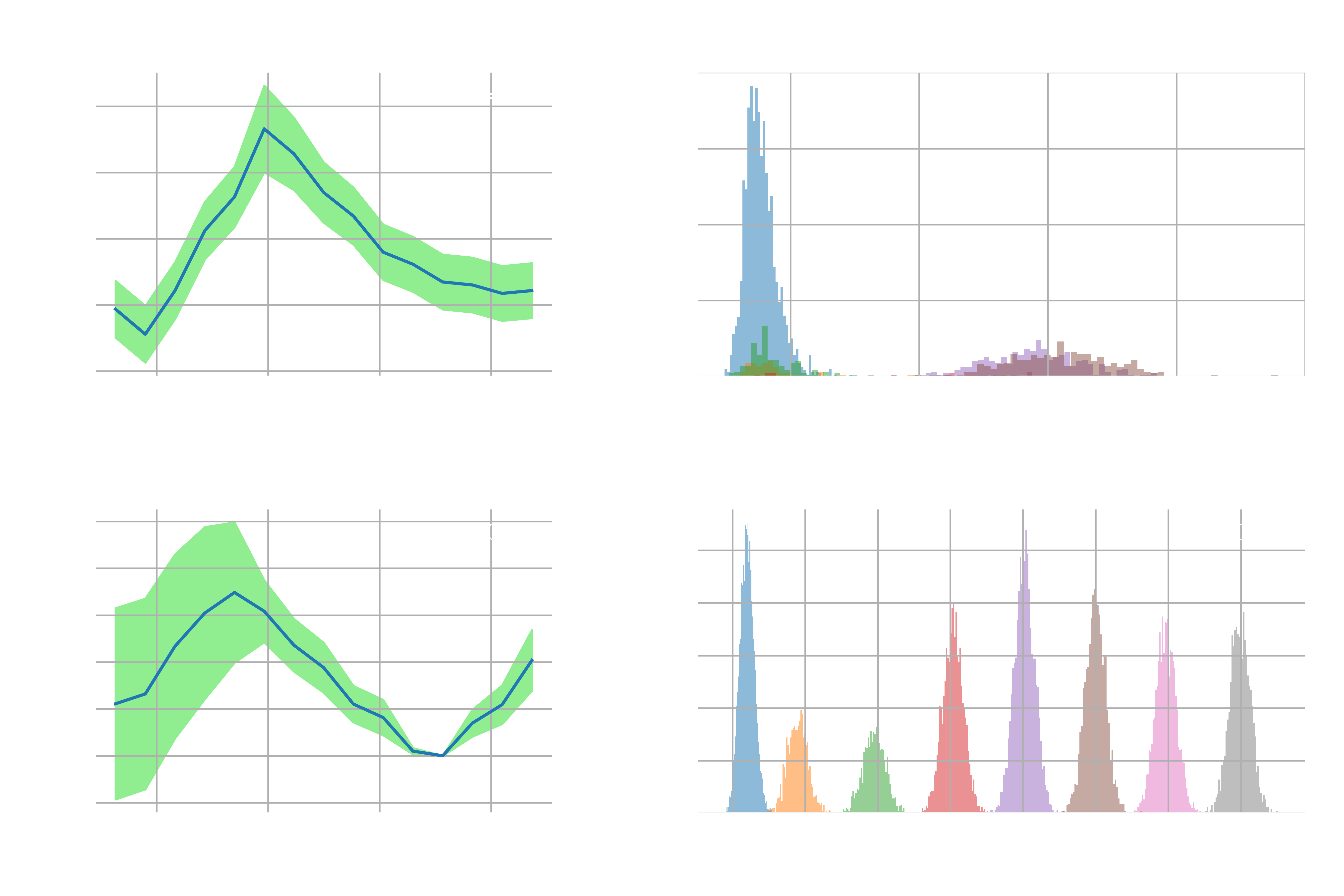
In the first case, where the force constant was set to
there was poor sampling/overlap in the region between the two metastable states, which corresponds to where the free energy barrier is. On the other hand, when the force constants were all set to
In a nutshell, the exercise above indicates that
Intuitively, we know that the spread of the CV distribution should be smaller given a large foce specified in the harmonic potential because the energy penalty incurred by the deviation from the desired center is larger, but if you wonder if there is a mathematical relationship between the two, please keep reading.
For a one-dimensional simple harmonic potential with a force constant
For example,
(However, for more complicated system, such a simple approximation may not apply.)
2.5.2. A note on common collective variables
In the example above, we used ion-pair distance to characterize the dissociation of NaCl. Such distance-based metrics are usually useful in describing the molecular event of interest. Common examples include the end-to-end distance of a folding protein, the center-of-mass distance between a receptor protein and its ligand, the distance between two sets of residues on both sides of the gate of a peptide transporter, and so on. In these cases, the biasing potential is essentially a distance restraint, though in GROMACS umbrella sampling, such restraints are not
More applications of umbrella sampling as an exercise?
3. Takeaways and concluding remarks
In conclusion, using umbrella sampling, we were able to estimate the free energy as a function of ion-pair distance of NaCl. Since its proposal, umbrella sampling has been used to study a wide variety of systems and phenomena (e.g., ligand-receptor binding and protein folding) and has many variations. For example, adaptive umbrella sampling (AUS)
more flexible
Finally, here is a list of takeaways from the article:
- An umbrella sampling simulation is composed of 2 steps:
- A pulling simulation: A simulation that is used to generate configurations at different CV values.
- Production runs: A bunch of simulations that fix configurations at different CV values to force the exploration of the CV space.
- The force constant for the pulling simulation does not really matter as long as it is strong enough to pull the pull group away.
- The force constant for the productions should be large enough to pin down the configurations but small enough to have wide probability distributions for each configuration.
- We should always decorrelate samples before performing MBAR.
- MBAR can estimate the free energy surface as a function of the chosen CV rigorously.
4. Supplementary materials
Here is a list of links to the supplementary notes in this article:
- Supplementary note: Position restraints implemented in GROMACS
- Supplementary note: Why is it important to have overlap between neighboring windows?
- Supplementary note: Other common collective variables
- Supplementary note: Generating an
.itpfile using the GROMACSgenrestrcommand
For those who favor video-based learning, I invite you to watch a recorded lecture of mine on umbrella sampling, delivered at the 3rd i-CoMSE workshop on advanced sampling methods. (Note that in the video I defined a mobile group and a pull group in the example, but a more common/correct way (adopted here) is to define pull groups and then select one of them to apply position restraints to.)
I’m also planning on writing blogposts about 2D umbrella sampling and applying different free energy estimators to umbrella sampling data, so please stay tuned if you’re interested!
Torrie, G. M.; Valleau, J. P. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J. Comput. Phys. 1977, 23 (2), 187–199. ↩︎
Kästner, J. Umbrella Sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1 (6), 932–942. ↩︎
Kumar, S.; Rosenberg, J. M.; Bouzida, D.; Swendsen, R. H.; Kollman, P. A. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13 (8), 1011–1021. ↩︎
Kirkwood, J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3 (5), 300–313. ↩︎
Bennett, C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J. Comput. Phys. 1976, 22 (2), 245–268. ↩︎
Shirts, M. R.; Chodera, J. D. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J. Chem. Phys. 2008, 129 (12), 124105. ↩︎
Tan, Z.; Gallicchio, E.; Lapelosa, M.; Levy, R. M. Theory of Binless Multi-State Free Energy Estimation with Applications to Protein-Ligand Binding. J. Chem. Phys. 2012, 136 (14). ↩︎
Zhang, B. W.; Xia, J.; Tan, Z.; Levy, R. M. A Stochastic Solution to the Unbinned WHAM Equations. J. Phys. Chem. Lett. 2015, 6 (19), 3834–3840. ↩︎
Ding, X.; Vilseck, J. Z.; Brooks, C. L., III. Fast Solver for Large Scale Multistate Bennett Acceptance Ratio Equations. J. Chem. Theory Comput. 2019, 15 (2), 799–802. ↩︎